Mi a másodrendű származék

A funkció összetett, ha leírható függvényében az y = f [φ (x)], ahol y = f (u), au = φ (x) gdeupromezhutochny érv. Bármilyen bonyolult függvénye lehet kifejezni elemi funkciók (egyszerű) a köztes érveit.

Egyszerű funkciók: Szövődmények:

y = x 2 y = (x + 1) 2; u = (x + 1); y = u 2;

y = sinx; y = sin2x; u = 2; y = Sinu;

y = e x e y = 2, u = 2; y = e u;

lnh y = y = ln (x + 2); u = x + 2; y = lnu.

Az általános szabály különbségtétel egy összetett függvény csökkentése miatt tétel bizonyítás nélkül.

Ha a funkció u = φ (x) van proizvodnuyuu'x = φ '(x) x pontban, a függvény y = f (u) származék u'u = f' (u) a megfelelő tochkeu, a származék összetett függvény az y = f [φ (x)] egy olyan ponton x adja meg: y'x = f '(u) · u' (x).

Gyakran használt kevésbé pontos, de rövid megfogalmazása ennek a tételnek: valamely egy összetett függvény a termék származék közbenső változó a származék közbenső változó a független változó.

Példa: y = sin2x 2; u = 2 2; y = Sinu;

3. A származék a másodrendű. Mechanikus értelmében a második derivált.

A függvény deriváltját y = f (x) nevezzük elsőrendű-származék vagy egy származéka az első függvény. Ezt a származékot az X függvényében, és lehetséges, hogy különbséget újra. A származék a származék az úgynevezett második sorrendű származék vagy második derivált. Ezt jelzi: az "x - (y két stroke által X); f" (x) - (EF kétdimenziós bar X); d 2 y / dx 2 - (TE két Y a Te X kétszer); d 2 f / 2 dx - (TE két X eff a de kétszer).

Meghatározásán alapul, a második derivált, írhatunk:

A második derivált, viszont az X függvényében, és ez lehet, hogy különbséget, és kap egy harmadrendű, stb

Mechanikus értelmében a második derivált magyarázata alapján pillanatnyi gyorsulás, amelyet az jellemez, alternáló mozgást.

Ha S = f (t) - az egyenlet a mozgás, to = S't; ASR. =

;

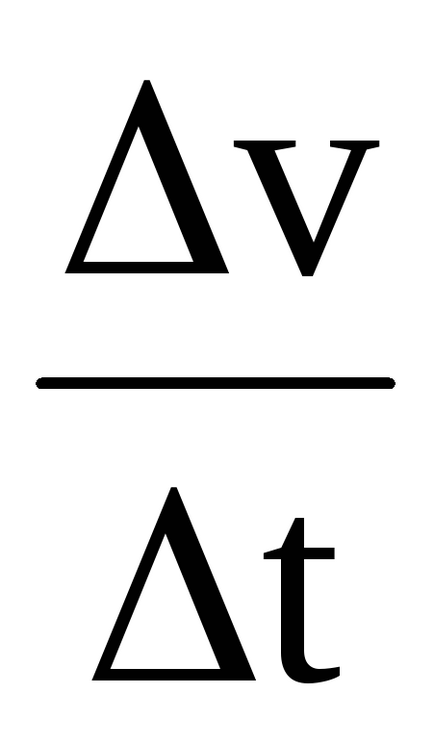
amgn. =

aSR = = 't; amgn. = 't = (S't) „t = s„tt.

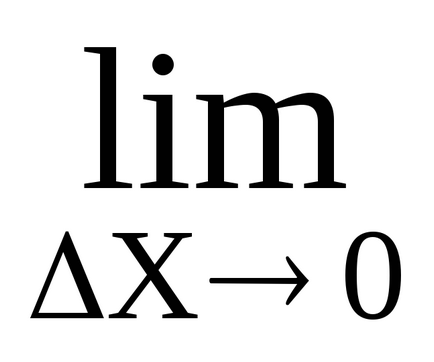
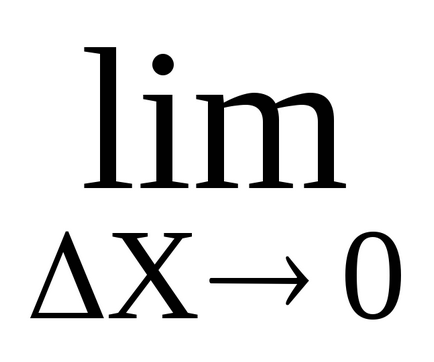
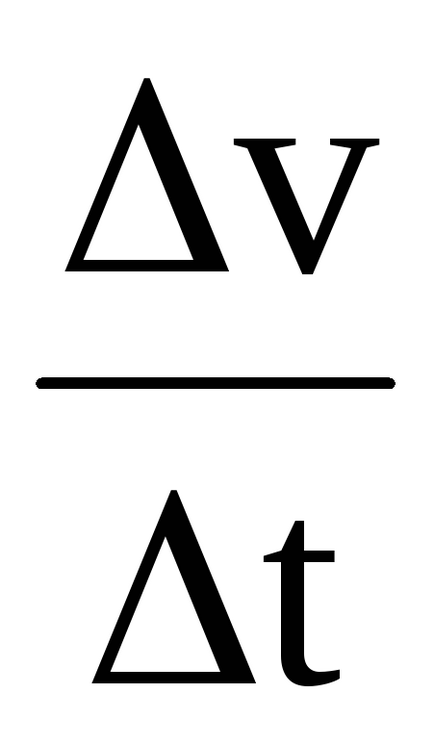
Így a második deriváltja az út adott időben megegyezik a pillanatnyi gyorsulását alternáló mozgást. Ez a fizikai (mechanikai) értelemben a második derivált.

Példa: Legyen a lineáris mozgás az anyag pont bekövetkezik zakonuS = t 3/3. A gyorsulás az anyag pont úgy definiáljuk, mint a második derivált S "tt: a = S" tt = (t 3/3) „= 2t.

4. differenciálmű működését.

A koncepció a származékot szorosan kapcsolódik a fogalom a differenciális funkció, amely nagy gyakorlati használatára.

A f (x) egy származékát

= F „(x);

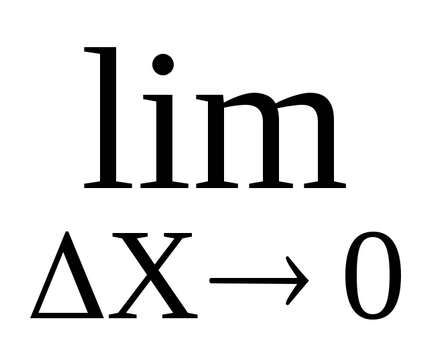
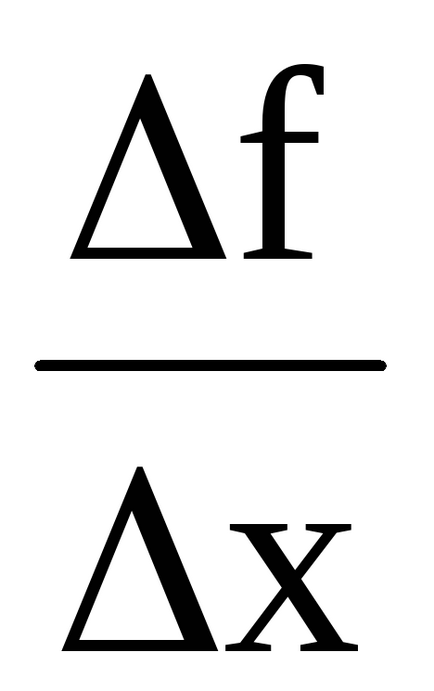
Egy tétele szerint (az elmélet nem) a kapcsolat végtelenül kicsi érték α (AH) (

α (AH) = 0) a-származék:= F '(x) + α (AH), ahol Af = f' (x) Ah + α (AH) · Ah.

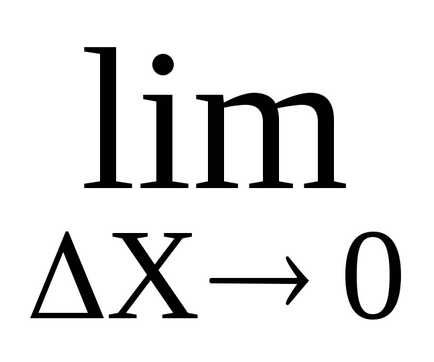
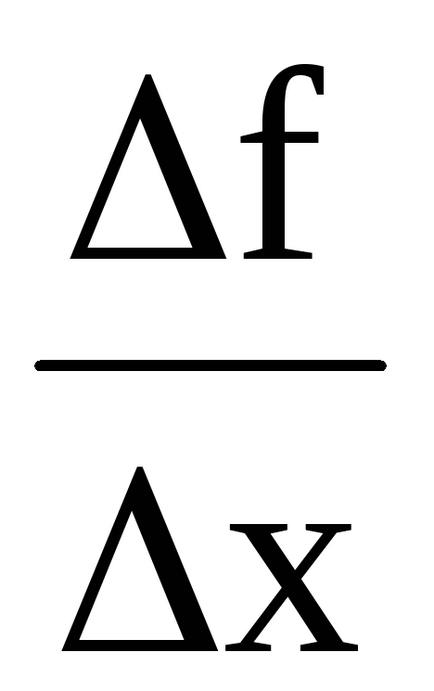
Az utolsó egyenlőség azt jelenti, hogy a növekmény funkció áll összeg minden kifejezést, amelynek egy végtelenül mennyiség, amikor Ah → 0.

Mi határozza meg a sorrendben kicsinysége minden végtelenül ezen összeg tekintetében végtelenül Ah:

Következésképpen, infinitezimális f (x) Ah és Ah azonos nagyságrendű.

Következésképpen, egy végtelenül kicsi mennyiség α (AH) Ah van egy magasabb rendű kicsinység viszonyított infinitezimális értéket Ah. Ez azt jelenti, hogy a kifejezéseket a második kifejezés Af α (AH) Ah gyorsan konvergál 0, amikor Ah → 0, mint az első ciklus f „(x) Ah.

Ez az első kifejezés f „(x) az úgynevezett differenciális Ah funkciót egy x pontban. Ez jelöli dy (Te y) ilidf (de ef). Így, dy = df = f '(x) ilidy AH = f' (x) dx, mivel differentsialdh egyenlő saját argumentum növekmény H (ha formuledf = f „(x) dx feltételezték, hogy az f (x) = x, akkor poluchimdf = dx = x'h Ax, nox'h = 1, t.e.dx = AH). Így a differenciál a funkció a termék ennek a funkciónak az eltérés érv.

Analitikai eltérés értelme az, hogy az eltérés a funkció - a fő része a növekmény Af funkciókat, lineáris tekintetében az érvelés Ah. Differenciál függvény különbözik a növekmény funkció végtelenül α (AH) Ah magasabb rendű Ah. Valóban Af = f „(x) Ah + α (AH) és Ah Af = df + α (AH) Ah; otkudadf = Δf- α (AH) Ah.

Példa: y = 2x 3 + x 2, dy = dy = u'dh = (2x 3 + x 2) „x dx = (6x 2 + 2) dx.

Elhanyagolása infinitezimális α (AH) Ah magasabb rendű Ah. kapjunk df≈ Δf≈ f „(x) dx azaz eltérés funkciót lehet használni, hogy közelítő számítást a növekmény funkciót, mivel egy eltérés általában könnyebben kiszámításához. A differenciális lehet alkalmazni, hogy a közelítő kiszámítása a függvény értéke. Nézzük ismert funktsiyay = f (x) és annak származéka az x. Meg kell találni az értéke f (x + Ah) a legközelebbi pont (x + Ah). Ehhez használja a közelítő egyenlet Au ≈dyili Au ≈f „(x) · Ah. Tekintettel arra, hogy Au = f (x + Ah) -f (x), poluchimf (x + Ah) -f (x) ≈f „(x) · dx, otkudaf (x + Ah) = f ( x) + f „(x) · dx. Az így kapott általános képletű megoldja a problémát.