Származékok magasabb rendű - számítási példákban

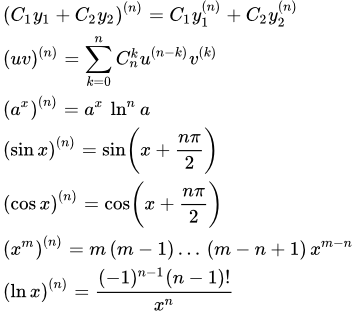
A példák a számítás a származékok magasabb rendű explicit funkciókat. Ez hasznos kiszámításához általános képletű n-ed rendű.

Itt azt az esetet, amikor az y változó függ az x változó kifejezetten:
.
Differenciálása a funkciója a x változó. egy származéka az elsőrendű, vagy egy származéka:
.
Az eredmény egy új funkció. amely egy származéka egy függvény. Differenciálás ez az új funkció az x változó. egy származéka a második sorrendben:
.
Differenciálás jellemző. hogy készítsen a harmadik rend:
.
És így tovább. Differenciálása az eredeti funkciót n-szer, megkapjuk a származékot n rend vagy n-edik-származék:
.

Származékok jelölhetjük stroke, római számok, arab számokkal zárójelben vagy frakció különbségek. Például, származékai harmadik és negyedik érdekében a következőképpen jelöljük:
;
.

Az alábbiakban olyan formulák, amelyek hasznosak lehetnek kiszámításához származékok nagyobb megrendeléseket.

Hasznos általános képletű n-ed rendű

A derivatív összegtől funkciók:
.
ahol - állandó.

Leibniz képletű származékot termék két funkciója van:
.
ahol
- binomiális együtthatók.

Keresse származékai az első és másodrendű következő funkciókat:
.

Megtaláljuk a származék az elsőrendű. Mi végre állandó jele az általános képletű és származékainak alkalmazására a táblázatban:
.
Mi a szabály alkalmazása során különbséget összetett funkció:
.
Itt van.
Mi a szabály alkalmazása során különbséget egy összetett függvényt, és használja a Point of származékok:
.
Itt van.

Tehát megtaláltuk a származék az elsőrendű:
.
Ahhoz, hogy megtalálja a származék a másodrendű, meg kell találnunk a származékot származék az elsőrendű, azaz a függvény:
.
Nem tévesztendő össze a jelöléssel jelöljük ezt a funkciót írni.
(A1.1).
Ezután, a második sorrendben származéka az eredeti funkció a függvény deriváltját.
.

Megtaláljuk a függvény deriváltját. Könnyebb csinálni a logaritmikus származék. Logaritmus (A1.1):
.
Most különbséget:
(A1.2).
De - ez állandó. Deriváltja nulla. Származik már talált. Ostalnve deriválhat az összetett függvény szabály differenciálás.
;
;
.
Mi helyettesíti az (A1.2):

Keresse meg a származék a harmadik rend:
.

Megtaláljuk a származék az elsőrendű. Ehhez veszünk ki egy állandó jele a származék, a táblázat segítségével a származékos és alkalmazza a szabályt találni valamely egy összetett függvény.

Itt van.
Tehát megtaláltuk a származék az elsőrendű:
.

Mi található a második derivált. Ehhez találunk a származéka. Képletének alkalmazásával származék frakciókat.
.
A származék a másodrendű:
.

Most azt látjuk, a szükséges harmadik deriváltak. Ahhoz, hogy ezt elérjük, különbséget.
;
;

A származék harmadik rend
.

Keresse meg a származéka hatodrendű az alábbi funkciók:
.

Ha megnyitja a konzolok, akkor egyértelmű, hogy az eredeti funkció a polinom foka. Írunk azt a formáját egy polinom:
.
ahol - az állandó együtthatók.

Ezután alkalmazzák a képlet n-edik származékát a hálózati funkció:
.
Egy hatodik érdekében származék (n = 6), van:
.
Ez azt mutatja, hogy mikor. Ha van:
.

A következő képlet a származékos funkcióit összege:

Így, hogy megtalálják a származéka hatodrendű az eredeti funkció, meg kell csak megtalálni a polinom együtthatót a legmagasabb fokozatot. Helye szorozni a legnagyobb hatalmak a terméket az összeg az eredeti funkció:

Megtalálja az N-edik függvény deriváltját
.

Megtalálja az N-edik származék az alábbi funkciók:
.
ahol - állandó.

Ebben a példában a számítási alkalmazásával végezzük komplex számok. Tegyük fel, hogy valamilyen komplex függvény
(A5.1).
ahol - egy függvény a valós x változó;
- az imaginárius egység.
Differenciálás (A.1) n alkalommal, van:
(A5.2).
Néha könnyebb megtalálni az n-edik függvény deriváltját. Ezután az n-edik származékot x definiált, mint a valós és képzetes része az n-edik származékot.
;
.

Alkalmazzuk ezt a módszert, hogy megoldja a példa. Tekintsük az
.
Itt alkalmazva Euler-képlet
.
és bevezette a jelölést
.
Ezután az n-edik származéka az eredeti függvényt a továbbiakban adjuk meg:
.

Azt találjuk, az n-edik függvény deriváltját
.
Ehhez alkalmazzuk a képlet:
.
A mi esetünkben,
.
majd
.

Tehát azt találtuk, az n-edik származékot a komplex funkció.
.
hol.
Keressünk egy igazi része a funkciót.
Ehhez jelenthet komplex szám exponenciális formában:
.
ahol;
;.
majd
;

Let.
Aztán;
.
Amikor.
.
.
.
És megkapjuk a képletű N-edik származékot koszinusz:
.