A vektor a területen 1

Definíció és variációk

euklideszi térben

Azaz minden egyes pontot a térben van leképezve egy vektor (a vektor mező értéke egy adott térbeli pontban). Általában ezt a vektort eltér a különböző térbeli pont, azaz általában vektormez® vállal különböző értékeket különböző pontjain az űrben. Minden egyes pont a mező vektor egy bizonyos méretű és bizonyos (kivéve azokat az eseteket, amikor a mező nullává válik) irányába ezt a helyet [3].

• A szakirodalomban (különösen idősebb, valamint fizikai) képest a vektor mező egy teret ürügyként (azaz úgy beszélnek, és a térben mezőt, és egy olyan területen a térben).

sokféleség

Általánosabb esetben, ha az eredeti tér egy sokrétű. vektor mező kerül meghatározásra egy része a tangens köteg Egy adott szerelvény, azaz a leképezés minden pont, ami p társítja a vektor X p> a pontbeli p.

A fizikában a vektor kifejezés mezőben. mellett közös értéke a fent leírt módon, különleges jelentéssel bír, főként tekintetében az alapvető területeken (cm. alább). A jelentése ennek fogyasztása csökken, hogy az a tény, hogy az alapvető fizikai mezők által minősített jellege a potenciális, és az egyik ilyen típus - vektor mezőben (vagy az elektromágneses mező gluon).

Jelöli a vektor mező általában csak összhangban elfogadott megállapodások vektorok által

• fizika erre általánosan használt félkövér betűvel vagy egy nyíl fölött, például
  • E> vagy v → >>;
  • 4-vektorok - hagyományos index rekord, mint az A i>;
• A matematikai irodalomban általában, minden vektor és vektor területeken különösen nincs közös speciális szimbólumok.

Gyakran kifejezetten támaszkodás egy térbeli pontban. [4] például:

B (p). (P),> ahol p - szimbolikus megjelölése egy térbeli pontban,

Általában elegendő hivatkozási vektor mező függvényében a koordináták a térben, amelyben a mező beállítása, például:

vagy (a mező, az idő-függő):

Alapjai Analitikai elmélet erőterek által kifejlesztett Maxwell. Gibbs és Heaviside második felében a XIX.

Különös esetek vektormezők

Vector mezőket a sorban

Minden valós értékű függvény egy valós változó lehet értelmezni, mint egy egydimenziós vektor mezőben.

Vector területeken a síkban

Vector mezők háromdimenziós térben

A háromdimenziós térben van értelme a következő jellemzők vektormez®

ahol a dot jelöli a skalár termék, dl> - egy vektor eleme a görbe pálya, amelynek mentén az integráció, F τ> - vetítés F> a (pozitív) érintő a görbe pálya, dl - skalár pályaelem (hossz elem), a C - specifikus görbe - integráció útján (általában támaszkodnak elég sima). Talán a legegyszerűbb fizikai prototípus az integrál a munka az erő F>. ható az a pont, ahogy mozog a pontot előre meghatározott úton.

- az integrál egy zárt áramkör:

ahol integrandus egybeesik ismertetett fölött, és a különbség abban rejlik az integráció útján C. amely ebben az esetben le van zárva a meghatározás, mivel jelzi egy kört az integrál jel.

F (R) (\ mathbf)> s- a felület úgy definiáljuk, mint az integrál S:

ahol F n> - vetítési mező vektor mentén felületre merőleges, d S> - «vektorelemet felület”, definíció szerint a készülék normál vektor, szorozva a d S. A legegyszerűbb példa Ennek a kialakításnak az a térfogat áthaladó folyadék felületi S., míg az áramlási sebesség az F.

derivált

Az analóg a-származék egy vektor mező hat tenzor parciális (Jacobi), amely derékszögű koordináta a következő:

- a nyoma a tenzor-származékok. Ez nem függ a koordinátarendszer (invariáns koordináta transzformáció, skalár), és a derékszögű koordináta alábbi képlettel számítottuk ki:

Ez ugyanaz a kifejezés felírható egy szimbolikus szereplő nabla

Gauss-tétel Ostrogradskii lehetővé teszi, hogy kiszámítsa az áramlási vektor mező használatával térfogati integráljával divergenciáját területén.

- a jellemző vektor örvény a vektor komponense mező. Ez a vektor koordinátái:

Az egyszerűség kedvéért, akkor tárolja a hagyományosan képviselik a rotor, mint a vektor termék:

- a legfontosabb és egyszerű művelet, amely lehetővé teszi számunkra, hogy a vektor területén skalármező. Alkalmazásával nyert ilyen műveletek egy skalármező f nevezzük, a gradiens vektor mező F:

vagy írásban keresztül Megfigy:

A vektor mezőt, amelynek divergencia nulla mindenhol, az úgynevezett szolenoid; leírható, mint egy rotor néhány más vektor mezőben.

A vektor a területen, a rotort, amely a nullával egyenlő bármely pontján az úgynevezett potenciális (lehessen beállítani); leírható mint egy gradiens egy skalármező (potenciális).

Van egy Helmholtz tétele. ha mindenütt a domain D y által meghatározott divergencia vektor mező és a rotor, akkor ezen a területen lehet leírni az összeget a potenciál és a szolenoid területen.

A vektor a területen, ahol a divergencia, és a rotor mindenhol nulla, az úgynevezett harmonikus; lehetséges egy harmonikus függvény.

vektor line

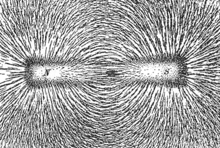
A mágneses erővonalak

Integrál görbe (is - egy vektor vonal erőterek - erőátviteli vezeték sebességterének mozgás egy folyadék - áramlási utat; .. Az első kifejezések közös, a másik - ezek szinonimák szerinti összefüggésben) a mezőt F (R) (\ mathbf) > ez egy görbe r = r (t) = \ mathbf (t)>. érintőleges amely minden ponton egybeesik a görbe érték mezőbe:

Ahhoz erőtér erővonalai egyértelműen jelzik az irányt a hatása terén erők.

Ha kellően kistérség a tér területén soha elenyészik, hogy az egyes pont ez a régió halad egy és csak egy erővonal. A pont, ahol a vektor mező nulla - különleges saját tér irányában nincs meghatározva, és a viselkedését a távvezetékek környezetében ezeket a pontokat különböző lehet: lehetséges, egy szinguláris pont halad végtelen számú erővonalakat, de lehetséges, hogy az ember nem adja át.

A vektor mező hívják teljes. ha annak szerves görbékkel az egész sokaság.

Vektor mező a n-dimenziós térben

Minden felsorolt ​​vektor mezők háromdimenziós térben szerkezetű és tulajdonságú közvetlenül általánosítható tetszőleges véges teret n dimenziós.

A legtöbb ilyen általánosítások egészen triviális, kivéve meghatározó rotor. a korrekt konstrukcióra, amelyek tetszőleges n-dimenziós esetben, szemben a három-dimenziós, szükséges, hogy egy külső. helyett egy vektort (melyet csak a három-dimenziós eset) a termék. Ha n = 2 a megfelelő művelet formájában történik pszeudo-skalár termék.

Továbbá, abban az esetben, tetszőleges n szüksége van egy bizonyos rendezett c meghatározás adatfolyam. Alapvető definíciók teljesen analóg átáramoljon az hiperfelület a dimenzió (n - 1).

A fizika, tipikus példái a vektor mezők erõterekhez (erőtér - térerősség (amely függ a térbeli helyzetét a szerv, amelyre az erő hat), vagy szorosan kapcsolódó erejét a térerősség).

Más jellemző példákban - a sebesség mező (például, folyékony vagy gáz áramlási sebessége), az elmozdulás mező (például, a deformált rugalmas közegben) és mások [5]. például, az áramsűrűség vektort. vektor energia áramlását vagy fluxus néhány anyagi részecskék (például, diffúzió) a hőmérséklet-gradiens vektort, koncentrációja vagy a nyomás stb, és így tovább.

Történelmileg, hidrodinamika volt óriási hatással megalakult a alapszerkezete vektor analízis és nagyon terminológiát. Így a hidrodinamikai eredetű fogalmak, mint a

• áramlási vektor mező,
• örvény (rotor) és a keringető a vektor mező,
• patak vonal

, és így vagy úgy, és még sokan mások (szinte minden egyikük, ha nem a hidrodinamikai eredetű hidrodinamikai értelmezés).

Különösen kifejezés használata a fizika

Általánosságban, a kifejezés a fizika vektormez® jelentése ugyanaz, mint a matematika fent leírt. Ebben az értelemben a vektormez® lehet nevezni bármilyen vektor-fizikai mennyiség függvényében egy pontot a térben, és gyakran attól is függ, hogy az idő.

Van azonban egy konkrét esetben a e kifejezés használata, azaz főleg a besorolás az alapvető fizikai területeken. Ebben az esetben a „vektor mező” azt jelenti, hogy a vektor mező (4-vektort vagy magasabb dimenzióba, ha van dolgunk, egy többdimenziós absztrakt elméleti modellek) a legalapvetőbb érték - potenciál. és nem annak származékai (térerősséget és t. o.). Például, a vektor mezők tartalmazzák az elektromágneses mezőt. a lehetséges, amely egy 4-vektor mező, míg a szilárdsága a jelenlegi szempontból, egy tenzor. A gravitációs mező neve ebben az értelemben a tenzor, mint a potenciál a tenzor területen.

Gyakorlati szinonimája a „vektor mező” ebben az értelemben a kifejezés vektor részecske a modern fizika (szintén tenyésztési ezek hasonló fogalmak vektor részecskéket nevezzük a gerjesztő vektor mező, vagy, hogy ez egy kicsit több hagyományos - vektor részecske egy kvantum a vektor mező). Egy másik gyakorlati szinonima - egy részecske spin 1. vagy centrifugálás 1 mező.

A figyelembe véve a osztályozásra (centrifugálás bozon alapvető mező) közvetlenül össze vannak kötve, néhány tulajdonságait a megfelelő mezők, például vonzza vagy taszítja a kölcsönhatás ezen a területen részecskék azonos töltésű (kapcsolatos ilyen típusú kölcsönhatás) azonos vagy ellentétes a töltést a részecske-antirészecske. A részecskék, amelyek kölcsönhatásba útján a vektor mező az azonos töltést visszaverik és vonzódnak az ellenkező, és a pár részecske - antirészecske ellenkező töltést egymáshoz (például különösen, abban az esetben az elektromágneses mező) - ellentétben a tulajdonságok a gravitációs erőtér és a gravitációs díjakat.

1. ↑ Elvileg, a vektor mező hasonló módon lehet meghatározni nem csak az euklideszi vagy pszeudo-euklideszi, hanem egy tetszőleges lineáris vagy affin teret, de általában a tér értjük még véges, és szándékunk, hogy ez határozza meg a belső termék (szükséges, hogy meghatározzuk a bázis vektorba műveletek vizsgálati eljárások, mint például a divergenciája vonalintegrál és így tovább) ..; A fizikai alkalmazások esetén gyakran szokásos fizikai háromdimenziós térben, vagy négydimenziós téridő.
2. ↑ Ez a formális matematikai definíciója nem tesz különbséget a fő tér és a tér térerősségvektorokat - ont állíthatunk elő más szaporodó száma (skalár). Abból a szempontból a fizika közötti terek van egy kis különbség, mivel a mező vektor, általában mért más egységek, így a személyazonosságát a fő tér és a tér térerősségvektorokat bizonyos mértékig önkényes (térerősségvektor képviselheti az alapvető helyet, de a hossza a vektor lenne feltételes). Azonban minden esetben, a szokásos szabványos A vektor bejuttatása mező fogalmát a dimenzióját e terek egybeesnek, sőt, a mező vektort csatlakozik a fő helyet abban az értelemben, hogy a villamos tér irányában vektor (ha nem nulla) teljes mértékben meghatározza a térben, amelyben az a területen van beállítva, hogy lehet felbontani a bázis (vagy vielbein) a fő tér, bár a hőtágulási együtthatók és nem fog dimenzió (abban az értelemben, fizikai egységek) száma is.
3. ↑ Ha egy nézett mező, az időfüggő (azaz változik az idővel), azt feltételezzük, hogy tart egy pontosan meghatározott értéket (nagyság és irány) az egyes térbeli pontban adott időben (és különböző időpontokban, ezek az értékek általában különböznek, és egy pont).
4. ↑ lehet, természetesen, ebben az esetben, ha szükséges, lehet járulékosan rendelkezésre, továbbá a funkcionális függés néhány más paraméterek, mint például az E → (R → Q.)> (>, Q),> ahol R → >>. - pontot a térben, Q - néhány további paraméter (például a töltés forrás).
5. ↑ Ezek a példák lehetnek többé vagy kevésbé alapvető, de elvileg gyakorlatilag bármilyen vektor, fizikai mennyiség, amely attól függ, hogy a koordinátákat lehet tekinteni, mint egy vektor mezőben.